二进制编码是指在二进制系统中表示的代码,与原始代码相比进行了修改。下面我们将会看到以下内容:
- 加权二进制系统
- 非加权编码
加权二进制编码
加权二进制编码是指符合位置加权原则的编码,数字的每个位置代表特定的权重。二进制计数序列就是一个例子
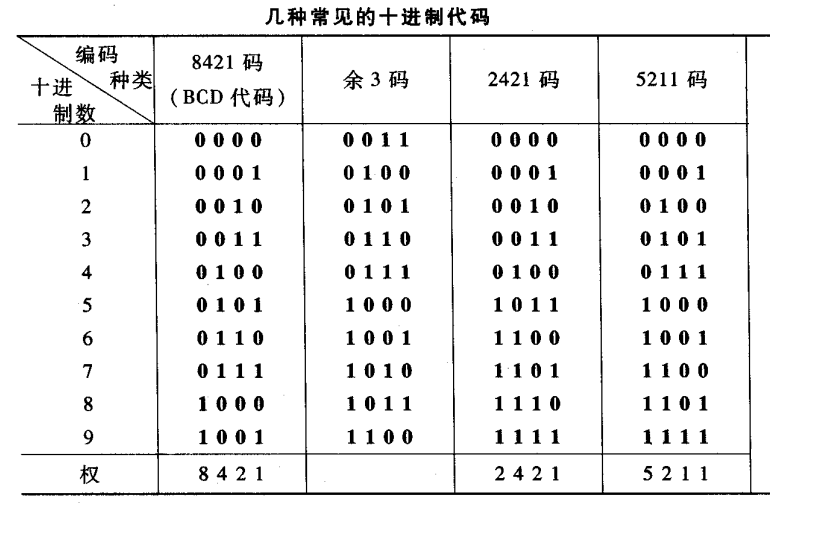
8421码/BCD码
8421码又称BCD码,是十进制代码中最常用的一种。
BCD(二进制编码十进制)是二进制等价的直接赋值。
8421码是一种加权二进制码,常用于将十进制数字转换为二进制形式。它的名称来自于它的权重分配:8、4、2和1。
在8421码中,一个十进制数字被表示为4位二进制数。每个二进制位的权重与它的位置相关,从左到右依次是8、4、2和1。如果某一位为1,则将对应的权重加到结果中;如果为0,则不加。通过这种加权方式,可以将十进制数字准确地转换为二进制形式。
举例来说,十进制数7的8421码为0111,因为:
0×8 + 1×4 + 1×2 + 1×1 = 7
8421码广泛应用于数字系统中,如数字显示器、BCD码和数字编码转换器等领域。
例如:比特分配1001,可以通过其权重表示十进制数9,因为:
1×8 + 0×4 + 0×2 + 1×1 = 9
8421码中每一位数的权是恒定不变的,它属于恒权代码。
2421码
2421码是一种加权码,其权重为2、4、2和1。一个十进制数以4位二进制形式表示,总的四位权重是2 + 4 + 2 + 1 = 9。因此,2421码表示从0到9的十进制数。
2421码是一种加权二进制码,用于将十进制数字表示为二进制形式。它的名称源自它的权重分配:2、4、2和1。
在2421码中,一个十进制数字被表示为4位二进制数。每个二进制位的权重与它的位置相关,从左到右依次是2、4、2和1。如果某一位为1,则将对应的权重加到结果中;如果为0,则不加。
举例来说,十进制数9的2421码为1001,因为:
1×2 + 0×4 + 0×2 + 1×1 = 9
2421码可以表示从0到9的十进制数字。它通常用于数字系统中,例如数字显示器和数字编码转换器。
2421码中每一位数的权是恒定不变的,它属于恒权代码。
5211码
5211码 这是一种加权码,其权重为5、2、1和1。一个十进制数以4位形式表示,总的四位权重为5 + 2 + 1 + 1 = 9。因此,5211码表示从0到9的十进制数。
5211码中每一位数的权是恒定不变的,它属于恒权代码。
如果按8421码接成十进制计数器,则连续输入计数脉冲时,4个触发器输出脉冲对于计数脉冲的分频比从低位到高位依次为5:2:1:1.可见,5211码每一位的权正好与8421码十进制计数器4个触发器输出脉冲的分频比相对应。
反射编码
非加权码
非加权码是指没有位置加权的编码方式。也就是说,二进制数中的每个位置没有被赋予固定的值。
余3码
是由8421BCD码加上0011形成的一种无权码,由于它的每个字符编码比相应的8421码多3,故称为余三码。余3码是一种非加权码,用于表示十进制数。该编码得名于每个二进制码都是对应的8421码加上0011(3)的事实。
格雷码 (Gray Code, 也称灰码)
格雷码又称循环码,灰码。格雷码(Gray code)是由贝尔实验室的Frank Gray在1940年提出,用于在PCM(脉冲编码调变)方法传送讯号时防止出错,并于1953年三月十七日取得美国专利。 格雷码是一个数列集合,相邻两数间只有一个位元改变,为无权数码,且格雷码的顺序不是唯一的。
它表示的数值+1时,只会改变循环码的一个数位,而不像二进制码下因进位而改变若干数位:比如从7到8,二进制码要同时改变四位,而格雷码只会变一位。 格雷码是非加权码,因为比特位的位置不包含任何权重。灰码是一种反射型数字编码,具有特殊属性,即任何两个连续的数字编码只相差一个比特位。这也被称为单位距离码。在数字领域,灰码具有特殊的地位。
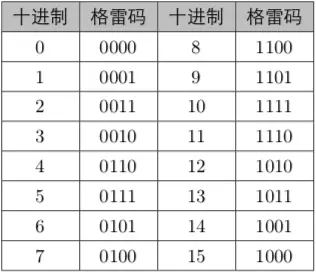
格雷码是一个叫弗兰克*格雷的人在 1953 年发明的,最初用于通信。格雷码是一种循环二进制码或者叫作反射二进制码。格雷码的特点是从一个数变为相邻的一个数时,只有一个数据位发生跳变,由于这种特点,就可以避免二进制编码计数组合电路中出现的亚稳态。格雷码常用于通信,FIFO 或者 RAM 地址寻址计数器中。
格雷码属于可靠性编码,是一种错误最小化的编码方式,因为虽然二进制码可以直接由数/模转换器转换成模拟信号,但在某些情况,例如从十进制的 3 转换为 4 时二进制码的每一位都要变,能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点,它在相邻位间转换时,只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。
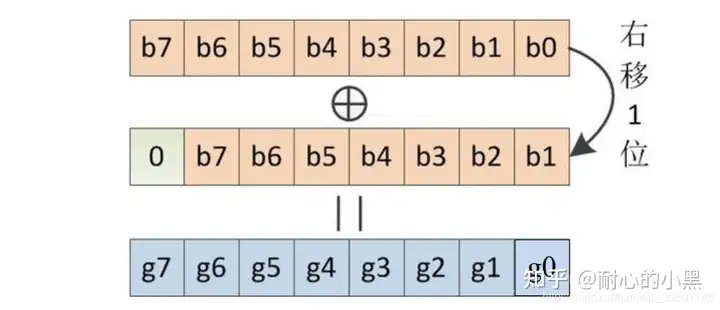
二进制计数编码从 0 到 15 的计数过程如下:
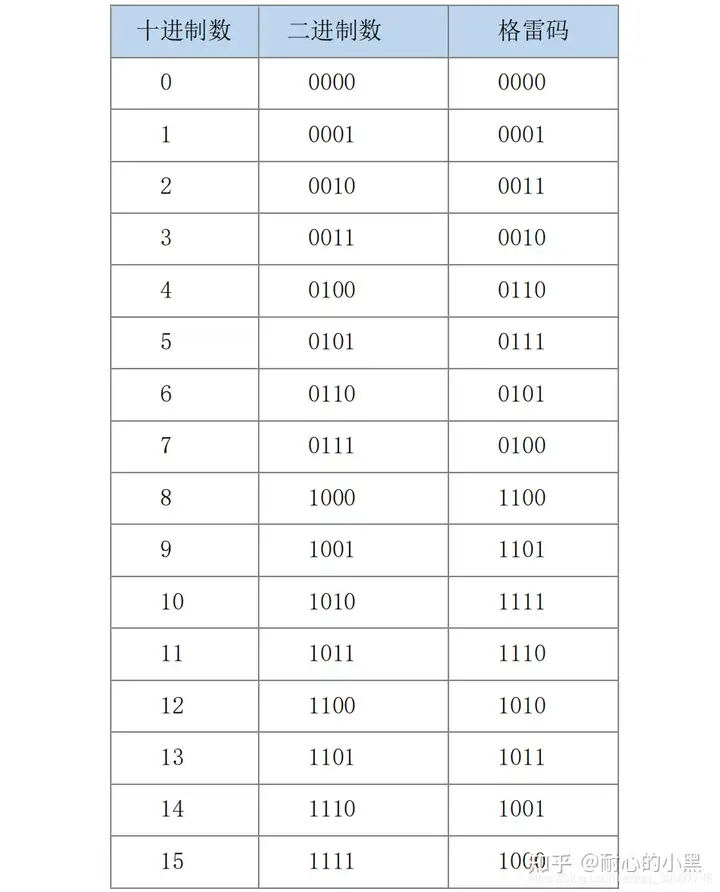
格雷码的转换原则如下:
- 1位格雷码有两个码字
- (n+1)位格雷码中的前2n个码字等于n位格雷码的码字,按顺序书写,加前缀0
- (n+1)位格雷码中的后2n个码字等于n位格雷码的码字,按逆序书写,加前缀1
- (n+1)位格雷码的集合 == n位格雷码集合(顺序)加前缀0 + n位格雷码集合(逆序)加前缀1
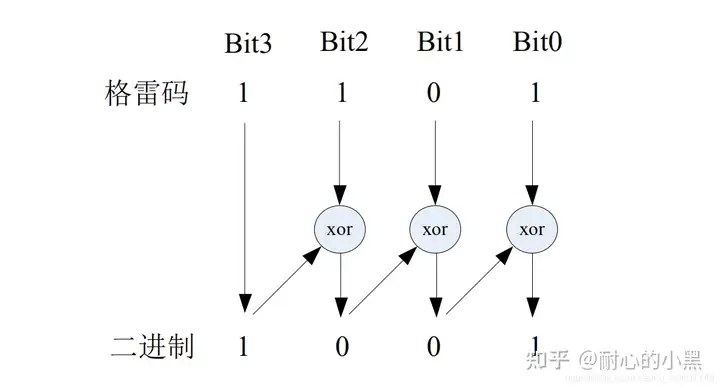
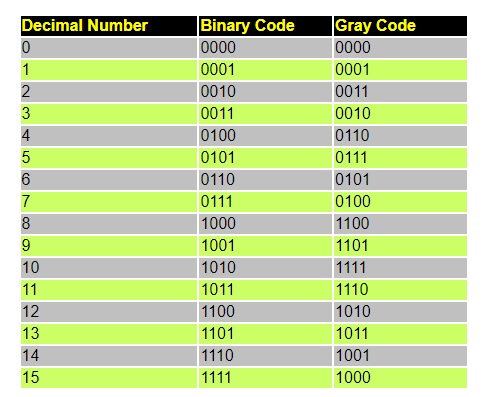
将二进制码转换为格雷码:
- 格雷码的最高有效位(MSB)与二进制码的最高有效位相同。
- 格雷码的次高有效位(MSB-1)是二进制码最高有效位(MSB)与次高有效位(MSB-1)的异或结果。
- 格雷码的第N-2位是二进制码的第N-1位与灰码的第N-2位的异或结果。
- 格雷码的第N位是二进制码的第N-1位与灰码的第N位的异或结果。
这样的转换过程逐位进行,直到所有位都转换完成。
余三码和8421码对比
余三码(余3码)【计算机】是由8421码加上0011形成的一种无权码,由于它的每个字符编码比相应的8421码多3,故称为余三码。BCD码的一种。
余三码是一种对9的自补代码,因而可给运算带来方便。其次,在将两个余三码表示的十进制数相加时,能正确产生进位信号,但对“和”必须修正。修正的方法是:如果有进位,则结果加3;如果无进位,则结果减3。
如, (526)10=(1000 0101 1001)余3码
8421码是中国大陆的叫法,即BCD代码。Binary-Coded Decimal,简称BCD,称BCD码或二-十进制代码,亦称二进码十进数。是一种二进制的数字编码形式,用二进制编码的十进制代码。这种编码形式利用了四个位元来储存一个十进制的数码,使二进制和十进制之间的转换得以快捷的进行。这种编码技巧,最常用于会计系统的设计里,因为会计制度经常需要对很长的数字串作准确的计算。相对于一般的浮点式记数法,采用BCD码,既可保存数值的精确度,又可免却使电脑作浮点运算时所耗费的时间。此外,对于其他需要高精确度的计算,BCD编码亦很常用。
余三码是在8421码的基础上,将每个代码都加上0011而形成。它的主要优点是执行十位数相加时可以产生正确的进位信号,而且给减法运算带来了方便。使用它进行加法运算的规则是当两个余三码数相加不产生进位时,则应该从结果中减去0011;产生进位时则一方面将进位信号送给高位余三码,另一方面本位还要执行加上0011的修正操作。
有权码,每位代码都有固定权值,结构形式与二进制数完全相同

