在介绍补码概念之前,先介绍一下“模”的概念:“模”是指一个计量系统的计数范围,如过去计量粮食用的斗、时钟等。计算机也可以看成一个计量机器,因为计算机的字长是定长的,即存储和处理的位数是有限的,因此它也有一个计量范围,即都存在一个“模”。如:时钟的计量范围是0~11,模=12。表示n位的计算机计量范围是0~2n-1,模= 2n;.“模”实质上是计量器产生“溢出”的量,它的值在计量器上表示不出来,计量器上只能表示出模的余数。任何有模的计量器,均可化减法为加法运算: 就是取反后加1。
假设当前时针指向8点,而准确时间是6点,调整时间可有以下两种拨法:一种是倒拨2小时,即8-2=6;另一种是顺拨10小时,8+10=12+6=6,即8-2=8+10=8+12-2(mod 12).在12为模的系统里,加10和减2效果是一样的,因此凡是减2运算,都可以用加10来代替。若用一般公式可表示为:a-b=a-b+mod=a+mod-b。对“模”而言,2和10互为补数。实际上,以12为模的系统中,11和1,8和4,9和3,7和5,6和6都有这个特性,共同的特点是两者相加等于模。对于计算机,其概念和方法完全一样。n位计算机,设n=8,所能表示的最大数是11111111,若再加1成100000000(9位),但因只有8位,最高位1自然丢失(相当于丢失一个模)。又回到了 00000000,所以8位二进制系统的模为28。在这样的系统中减法问题也可以化成加法问题,只需把减数用相应的补数表示就可以了。把补数用到计算机对数的处理上,就是补码 。
一、二进制
二进制和十进制一样,也是一种进位计数制,但是它的基数是 2。二进制表达式中 0 和 1 的位置不同,它所代表的数值也不同。例如,二进制数 0000 1010 表示十进制数 10。一个二进制数具有两个基本特点:两个不同的数字符号,即 0 和 1,逢二进一。
十进制与二进制数之间的转换
用计算机处理十进制数时,必须先把它转化为二进制数才能被计算机所接受;同理,计算结果应该将二进制数转换成人们习惯的十进制数。
十进制转换成二进制
把一个十进制转换为二进制的方法是:把被转换的十进制数反复地除以 2,直到商为 0 为止,所得余数(从末位读起)就是这个数的二进制表示,简单地说,就是 “除 2 取余法”。

二进制转十进制
要把二进制转换为十进制数,只要将二进制数按权展开求和即可。

二、数值型数据的表示
在计算机内数值型数据分成整数和实数两大类。数据都是以二进制的形式存储和运算的。计算机中的数字电路只能直接识别二进制数据,数的正(+)、负(-)号是不能被计算机识别的,为了让计算机能识别正、负号,就必须对符号进行编码,或者说把符号数字化。通常采用二进制数的最高位来表示符号,用 ”0“ 表示正数,”1“ 表示负数。
整数的表示
整数可分为无符号整数和有符号整数。在无符号整数中,所有二进制位全部用来表示数的大小;在有符号整数中,用最高位表示数的正负号,其他位表示数的大小。如果用一个字节表示一个无符号整数,其取值范围是 0 ~255。如果表示一个有符号整数,其取值范围是 -128 ~ 127。计算机中的地址常用无符号整数表示,可以用 8 位、16 位或 64 位来表示。
实数的表示
实数一般用浮点数表示,因为它的小数点位置不固定,所以称为浮点数。它是既有整数又有小数的数,纯小数可以看做实数的特例,例如,76.625,0.00345 都是实数,又可以表示为:
|
1 2 |
<span class="hljs-attribute">76</span>.<span class="hljs-number">625</span>=<span class="hljs-number">10</span>^<span class="hljs-number">2</span> ×(<span class="hljs-number">0</span>.<span class="hljs-number">76625</span>) <span class="hljs-attribute">0</span>.<span class="hljs-number">00345</span>=<span class="hljs-number">10</span>^-<span class="hljs-number">2</span> × (<span class="hljs-number">0</span>.<span class="hljs-number">345</span>) |
其中,指数部分用来指出实数中小数点的位置,括号内的一个纯小数。在计算机中一个浮点数由指数(阶码)和尾数两部分组成,阶码部分由阶符和阶码组成,尾数部分由尾符和尾数组成。其机内表示形式如下:

阶码用来指示尾数中的小数点应当向左或向右移动的位数;尾数表示数值的有效数字,其小数点约定在数符和尾数之间,在浮点数中数符和阶符各占 1 位,阶码的值随浮点数数值的大小而定,尾数的位数则依浮点数数值的精度要求而定。
三、原码、反码和补码
为运算方便,机器数有 3 种表示法,即原码、反码和补码。
原码
原码是一种计算机中对数字的二进制定点表示法。原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为 0,负数该位为 1(0 有两种表示:+0 和 -0),其余位表示数值的大小。举个例子,我们用 8 位二进制表示一个数,+12 的原码为 00001100,-12 的原码就是 10001100。
反码
一个数字用原码表示是容易理解的,但是需要单独一个位来表示符号位,并且在进行加法时,计算机需要先识别某个二进制原码是正数还是负数,识别出来之后再进行相应的运算。这样效率不高,能不能让计算机在进行运算时不用去管符号位,也就是让符号位参与运算。要实现这个功能,我们就要用到反码。
反码是一种在计算机中数的机器码表示。对于单个数值(二进制的 0 和 1)而言,对其进行取反操作就是将 0 变为 1,1 变为 0。正数的反码和原码一样,负数的反码就是在原码的基础上符号位保持不变,其他位取反。
| 十进制 | 原码 | 反码 |
|---|---|---|
| 6 | 0000 0110 | 0000 0110 |
| -3 | 1000 0011 | 1111 1100 |
下面我们来看一下,用反码直接运算会是什么情况,我们以 6 - 3 为例,6 - 3 等价于 6 + (-3)。
下面我们来看一下,用反码直接运算会是什么情况,我们以 6 - 3 为例,6 - 3 等价于 6 + (-3)。
|
1 2 3 4 5 6 |
6 - 3 ==> 6 + (-3) <span class="hljs-code"> 0000 0110 // 6(反码)</span> <span class="hljs-section">+ 1111 1100 // -3(反码) ----------------------</span> <span class="hljs-code"> 0000 0010 // (反码)</span> <span class="hljs-code"> 0000 0010 // 2(原码) </span> |
很明显通过反码进行 6 + (-3) 加法运算时,输出值比预期值差了一个 1。接着我们再来看下 1 + (-1) 的运算结果:
|
1 2 3 4 5 6 |
1 - 1 ==> 1 + (-1) <span class="hljs-code"> 0000 0001 // 1(反码)</span> <span class="hljs-section">+ 1111 1110 // -1(反码) ----------------------</span> <span class="hljs-code"> 1111 1111 // (反码)</span> <span class="hljs-code"> 1000 0000 // -0(原码)</span> |
由上可知 1 + (-1) 的运算结果为 -0,而我们预期的值是 +0。我们继续看个示例 0 + 0:
|
1 2 3 4 5 6 |
0 <span class="hljs-code">+ 0 ==> 0 +</span> 0 <span class="hljs-code"> 0000 0000 // 0(反码)</span> <span class="hljs-section">+ 0000 0000 // 0(反码) ----------------------</span> <span class="hljs-code"> 0000 0000 // (反码)</span> <span class="hljs-code"> 0000 0000 // 0(原码)</span> |
这里我们可以知道 -0 对应的原码是 1000 0000,而 +0 对应的原码是 0000 0000。虽然 -0 和 +0 代表的数值是一样的,但是在用原码和反码表示时它们是不同的。通过以上的多个示例,我们发现使用反码进行加法运算并不能保证得出正确的结果。原因是用一个字节表示数字的取值范围时,这些数字中多了一个 -0。为了解决反码出现的问题,就出现了补码。
补码
补码是一种用二进制表示有符号数的方法。正数和 0 的补码就是该数字本身。负数的补码则是将其对应正数按位取反再加 1。补码系统的最大优点是可以在加法或减法处理中,不需因为数字的正负而使用不同的计算方式。只要一种加法电路就可以处理各种有符号数加法,而且减法可以用一个数加上另一个数的补码来表示,因此只要有加法电路和补码电路即可以完成各种有符号数加法和减法,在电路设计上相当方便。
另外,补码系统的 0 就只有一个表示方式,这和反码系统不同(在反码系统中,0 有两种表示方式),因此在判断数字是否为 0 时,只要比较一次即可。
0的补码
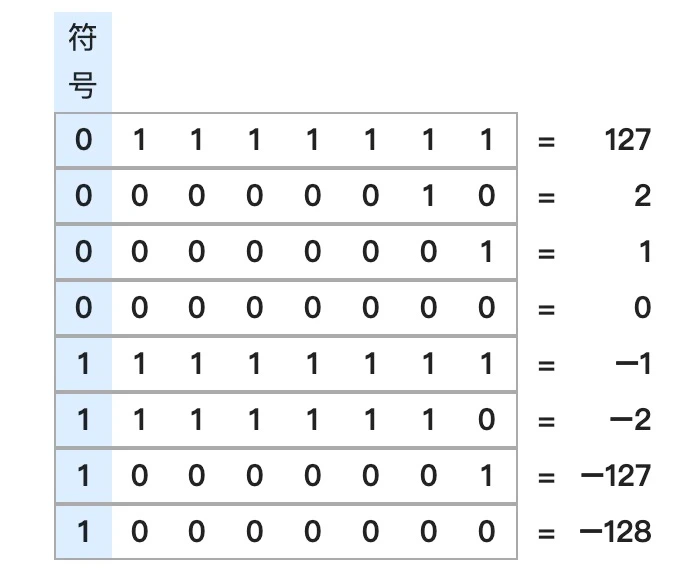
下图是一些 8 位补码系统的整数,它可表示的范围包括 -128 到 127,总共 256 个整数。
既然说补码可以解决反码在运算中遇到的问题,我们继续以 6 + (-3) 为例来验证一下这个结论。
既然说补码可以解决反码在运算中遇到的问题,我们继续以 6 + (-3) 为例来验证一下这个结论。
| 十进制 | 原码 | 反码 | 补码 |
|---|---|---|---|
| 6 | 0000 0110 | 0000 0110 | 0000 0110 |
| -3 | 1000 0011 | 1111 1100 | 1111 1101 |
6 + (-3) 以补码形式的计算过程如下:
|
1 2 3 4 5 |
6 - 3 ==> 6 + (-3) <span class="hljs-code"> 0000 0110 // 6(补码)</span> <span class="hljs-section">+ 1111 1101 // -3(补码) ----------------------</span> <span class="hljs-code"> 0000 0011 // 3(补码)</span> |
很明显这时我们得到了正确的结果,那么我们再来看一下以补码形式计算 1 - 1 的计算过程:
|
1 2 3 4 5 |
1 - 1 ==> 1 + (-1) <span class="hljs-code"> 0000 0001 // 1(补码)</span> <span class="hljs-section">+ 1111 1111 // -1(补码) ----------------------</span> <span class="hljs-code"> 0000 0000 // 0(补码)</span> |
可以发现,补码完美解决了反码的问题。
补码求原码
已知一个数的补码,求原码的操作其实就是对该补码再求补码 :
