JavaScript 递归函数

在本教程中，你将学习如何使用递归技术来开发 JavaScript 递归函数，即一个调用自身的函数。

 

---

JavaScript 递归函数简介

递归函数是一个会调用自身的函数，直到不再调用为止。这个技术称为递归。

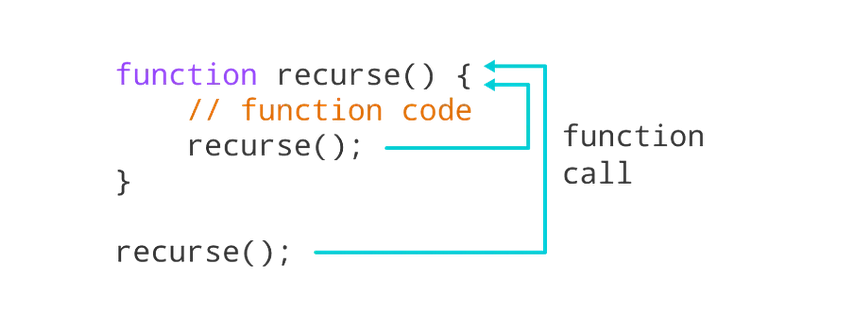
假设你有一个名为 recurse() 的函数。如果 recurse() 在其函数体内调用自身，那么它就是一个递归函数，如下所示：

递归函数总是有一个停止调用自身的条件。否则，它将无限地调用自身。

因此，递归函数通常如下所示：

通常，你使用递归函数将一个大问题分解为更小的问题。你通常会在数据结构（如二叉树和图）以及算法（如二分查找和快速排序）中找到递归函数。

---

JavaScript 递归函数示例

让我们看一些使用递归函数的示例。

1）一个简单的 JavaScript 递归函数示例

假设你需要开发一个函数，从指定的数字倒数到 1。例如，从 3 倒数到 1：

以下展示了 countDown() 函数：

这个 countDown(3) 只显示数字 3。

要从数字 3 倒数到 1，你可以：

1. 显示数字 3。
2. 调用 countDown(2)，显示数字 2。
3. 调用 countDown(1)，显示数字 1。

以下将 countDown() 更改为递归函数：

这个 countDown(3) 将运行，直到调用堆栈大小超出限制，如下所示：

因为它没有停止调用自身的条件。

倒数将在下一个数字为零时停止。因此，你添加一个 if 条件如下：

输出：

countDown() 似乎按预期工作。

然而，如 函数类型教程 中所述，函数的名称是对实际函数对象的引用。

如果函数名称在代码中的某处被设置为 null，递归函数将停止工作。

例如，以下代码将导致错误：

错误：

脚本的工作方式如下：

1. 首先，将 countDown 函数名称赋值给变量 newYearCountDown。
2. 其次，将 countDown 函数引用设置为 null。
3. 第三，调用 newYearCountDown 函数。

该代码导致错误，因为 countDown() 函数体引用了函数名称 countDown，而在调用函数时它已被设置为 null。

为了解决这个问题，你可以使用命名函数表达式，如下所示：

2）计算 n 个自然数的总和示例

假设你需要使用递归技术来计算从 1 到 n 的自然数之和。为此，你需要递归地定义 sum() 函数，如下所示：

基本情况（Base Case）：

• 该函数以一个 if 语句开始，检查 n 是否小于或等于 1。

• 如果 n 是 1 或更小，函数返回 n。这是基本情况，作为递归的终止条件。

递归情况（Recursive Case）：

• 当 n 大于 1 时，不满足基本情况；函数进入 if 语句之后的代码块。

• 函数返回 n 加上调用自身、参数为 n - 1 的结果。这就是递归发生的地方。

工作原理（How it Works）：

• 例如，当你调用 sum(3) 时，函数首先检查 3 是否小于或等于 1（不满足基本情况）。

• 因为不是基本情况，它计算 3 + sum(2)。此时它用参数 2 再次调用自身。

• 在下一次递归调用中（sum(2)），它计算 2 + sum(1)。

• 接着，在 sum(1) 的调用中，它达到基本情况并返回 1。

• 现在，之前的调用依次被解析：2 + 1 得到 3，3 + 3 得到最终结果 6。

终止（Termination）：

• 递归不断发生，将问题缩减为更小的子问题，直到达到基本情况为止。

• 一旦达到基本情况，函数开始回溯，将每一层递归的结果组合起来，直到获得最终结果。

总结

• 递归函数是一个会调用自身的函数，直到不再调用为止。
• 递归函数总是有一个停止调用自身的条件。