一个函数在它的函数体内调用它自身称为递归调用，这种函数称为递归函数。执行递归函数将反复调用其自身，在递归调用中，主调函数又是被调函数。执行递归函数将反复调用其自身，每调用一次就进入新的一层。
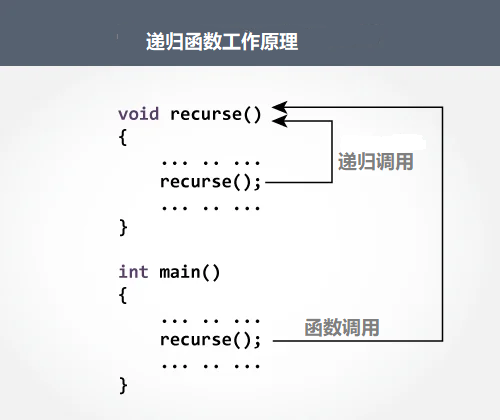
例如有函数 recurse 如下：
int recurse(int x)
{
int y;
z=recurse(y);
return z;
}这个函数是一个递归函数。但是运行该函数将无休止地调用其自身，这当然是不正确的。为了防止递归调用无终止地进行，必须在函数内有终止递归调用的手段。
常用的办法是加条件判断，满足某种条件后就不再作递归调用，然后逐层返回。
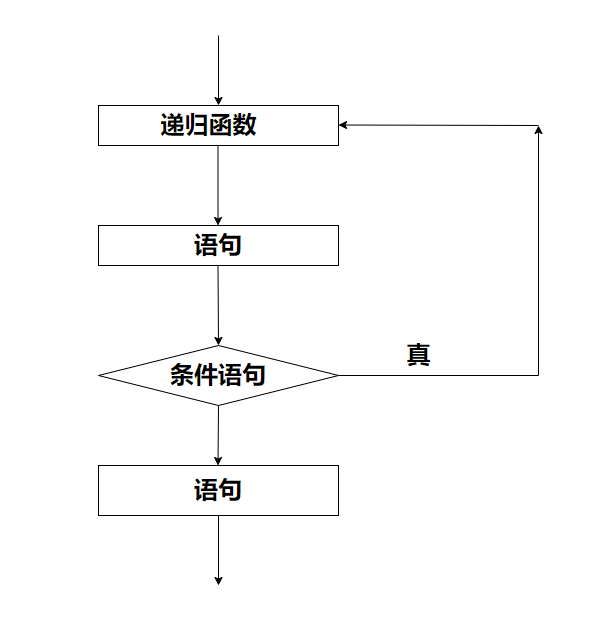
下面举例说明递归调用的执行过程。
执行递归函数将反复调用其自身，每调用一次就进入新的一层，当最内层的函数执行完毕后，再一层一层地由里到外退出。
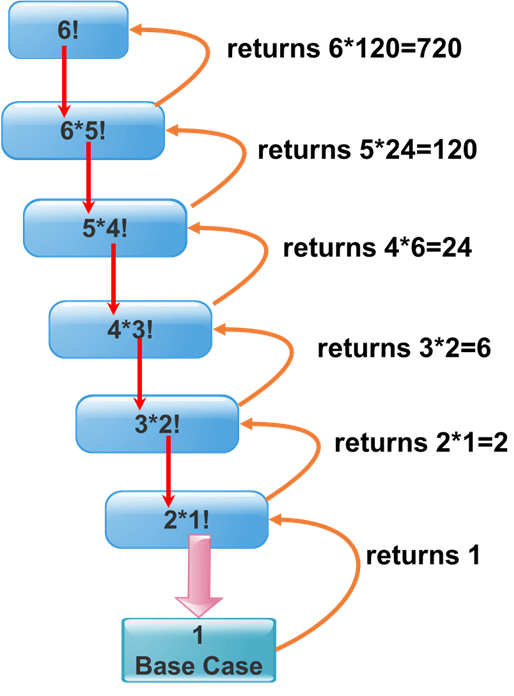
考虑一个数字的阶乘，其计算公式如下6！ = 6 * 5 * 4 * 3 * 2 * 1。重复计算fact*（fact-1）直到fact等于1。
例1.利用递归函数计算6的阶乘
#include <stdio.h>
int factorial(int number);
int main()
{
int x = 6;
printf("The factorial of %d is %d\n", x, factorial(x));
return 0;
}
int factorial(int number)
{
if (number == 1)
return (1); /* exiting condition */
else
return (number * factorial(number - 1));
}
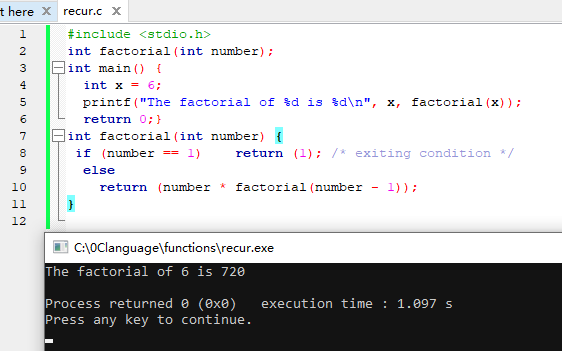
factorial() 就是一个典型的递归函数。调用 factorial() 后即进入函数体，只有当 n==1 时函数才会执行结束，否则就一直调用它自身。
由于每次调用的实参为 n-1，即把 n-1 的值赋给形参 n，所以每次递归实参的值都减 1，直到最后 n-1 的值为 1 时再作递归调用，形参 n 的值也为1，递归就终止了，会逐层退出。
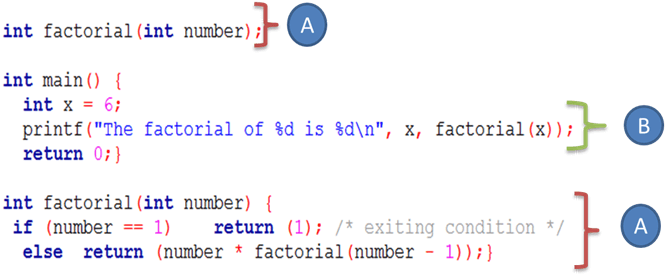
A. 声明一个函数，该函数接受一个整数参数并返回该参数的阶乘。此函数将调用自身并减少参数值直到退出或达到基本条件为止。当条件为真时，先前生成的值将彼此相乘，并返回最终的阶乘值。
B. 声明并初始化一个值为“ 6”的整数变量，然后通过调用阶乘函数来打印其阶乘值
考虑下图，以更深入地了解递归机制，该机制包括调用函数自身直至达到基本情况或停止条件，然后再收集先前的值：
例2.利用递归函数计算自然数之和
include <stdio.h>
int sum(int n);
int main() {
int number, result;
printf("Enter a positive integer: ");
scanf("%d", &number);
result = sum(number);
printf("sum = %d", result);
return 0;
}
int sum(int n) {
if (n != 0)
// sum() function calls itself
return n + sum(n-1);
else
return n;
}
结果
Enter a positive integer:3
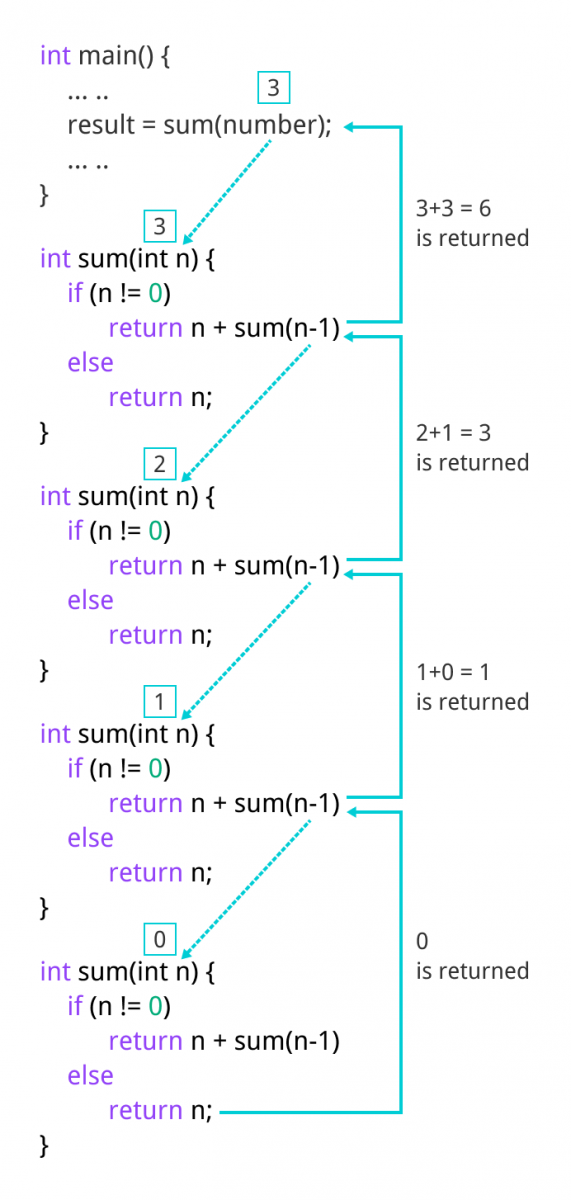
sum = 6最初，从 main() 函数调用 sum()，并将数字作为参数传递。
假设 sum() 中 n 的值最初是 3。在下一次函数调用期间，将 2 传递给 sum() 函数。这个过程一直持续到 n 等于 0。
当 n 等于 0 时，if 条件失败并执行 else 部分，最终将整数总和返回给 main() 函数。
例3.用递归法计算 n!
long ff(int n)
{
long f;
if(n<0) printf("n<0,input error");
else if(n==0||n==1) f=1;
else f=ff(n-1)*n;
return(f);
}
main()
{
int n;
long y;
printf("\ninput a inteager number:\n");
scanf("%d",&n);
y=ff(n);
printf("%d!=%ld",n,y);
}
递归的条件
每一个递归函数都应该只进行有限次的递归调用，否则它就会进入死胡同，永远也不能退出了，这样的程序是没有意义的。
要想让递归函数逐层进入再逐层退出，需要解决两个方面的问题：
- 存在限制条件，当符合这个条件时递归便不再继续。对于 factorial()，当形参 n 等于 0 或 1 时，递归就结束了；
- 每次递归调用之后越来越接近这个限制条件。对于 factorial()，每次递归调用的实参为 n – 1，这会使得形参 n 的值逐渐减小，越来越趋近于 1 或 0。
更多关于递归函数的内容
factorial() 是最简单的一种递归形式——尾递归，也就是递归调用位于函数体的结尾处。除了尾递归，还有更加烧脑的两种递归形式，分别是中间递归和多层递归：
递归函数也只是一种解决问题的技巧，它和其它技巧一样，也存在某些缺陷，具体来说就是：递归函数的时间开销和内存开销都非常大，极端情况下会导致程序崩溃。
更深阅读
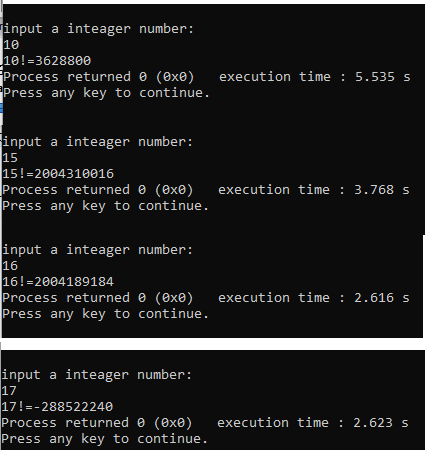
17！程序结果溢出是什么原因 ？
[content_control]
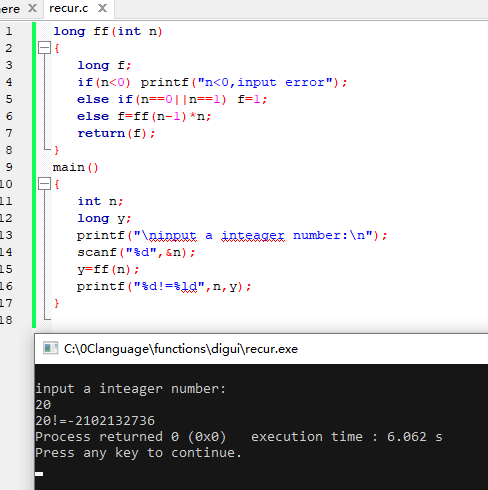
例4.用递归法计算 n!
unsigned long long int ff(int n)
{
unsigned long long int f;
if(n<0) printf("n<0,input error");
else if(n==0||n==1) f=1;
else f=ff(n-1)*n;
return(f);
}
main()
{
int n;
unsigned long long int y;
printf("\ninput a inteager number:\n");
scanf("%d",&n);
y=ff(n);
printf("%d!=%lld",n,y);
}
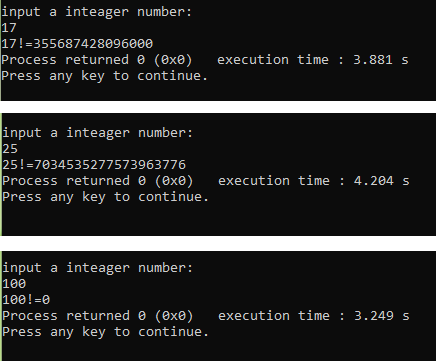
把计算阶乘的递归函数的调用类型改为unsigned long long int 型，就能够计算出17，25等的结果。
[/content_control]
例5. 用户给出一个数，求出其相应的斐波那契数列数
int Fibonacci(int n){
if (n <= 1)
return n;
else
return Fibonacci(n-1) + Fibonacci(n-2);
}
main()
{
int n;
int y;
printf("\ninput a integer number:\n");
scanf("%d",&n);
y=Fibonacci(n);
printf("%d Fibonacci Number =%d",n,y);
}
