二进制转十进制
任何二进制数都可以通过将二进制数中包含1的各个位置的权值相加来转换为十进制等价数。
|
Binary |
Decimal |
|
110112 |
|
|
24+23+01+21+20 |
=16+8+0+2+1 |
|
Result |
2710 |
|
Binary |
Decimal |
|
101101012 |
|
|
27+06+25+24+03+22+01+20 |
=128+0+32+16+0+4+0+1 |
|
Result |
18110 |
您应该已经注意到,该方法是找到每个包含1的位位置的权值(即2的幂),然后将它们相加。
十进制转二进制的方法
十进制转二进制的方法有两种:
- 反转二进制到十进制的方法
- 重复除法
反转二进制到十进制的方法
|
Decimal |
Binary |
|
4510 |
=32 + 0 + 8 + 4 +0 + 1 |
|
=25+0+23+22+0+20 |
|
|
Result |
=1011012 |
重复除法
“重复除法”方法将十进制转换为二进制,其步骤是反复将十进制数除以2,并记录余数,直到商变为零为止。然后,通过逆序读取余数来获得二进制等价数。
具体步骤如下:
- 将十进制数除以2。
- 记录余数。
- 使用步骤1中获得的商重复进行除法。
- 持续这个过程,直到商变为零。
- 通过逆序读取余数获得二进制等价数。
例如,让我们将十进制数13转换为二进制:
- 13 ÷ 2 = 6 余 1
- 6 ÷ 2 = 3 余 0
- 3 ÷ 2 = 1 余 1
- 1 ÷ 2 = 0 余 1
逆序读取余数,得到1101。
因此,十进制数13的二进制等价数为1101。
二进制和十进制之间的相互转化,请看:十进制和二进制的相互转换
二进制到八进制 / 八进制到二进制转换
从二进制到八进制转换:
- 将二进制数按照从右到左的顺序分组,每三位一组。如果最左边的组不足三位,则在左边补0。
- 将每个组转换为对应的八进制数。
- 将转换后的八进制数按照从左到右的顺序排列,得到最终的八进制数。
|
Octal Digit |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Binary Equivalent |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
100 111 0102 = (100) (111) (010)2 = 4 7 28
从八进制到二进制转换:
- 将八进制数中的每一位转换为对应的三位二进制数。
- 将这些三位二进制数按照从左到右的顺序排列,得到最终的二进制数。
例如,让我们从二进制数10111011转换为八进制数:
- 将二进制数按照三位一组分组:1 011 101 1
- 每个组转换为对应的八进制数:1 3 5 1
- 将转换后的八进制数排列起来:1351
现在,让我们从八进制数6752转换为二进制数:
- 将八进制数中的每一位转换为对应的三位二进制数:110 111 101 010
- 将这些三位二进制数排列起来:110111101010
因此,二进制数10111011的八进制等价数为1351,八进制数6752的二进制等价数为110111101010。
使用重复除法将十进制转换为八进制的方法
使用重复除法将十进制转换为八进制的方法如下:
- 将十进制数重复除以8,直到商为0,记录每次的余数。
- 逆序读取所记录的余数,即可得到对应的八进制数。
例如,我们来将十进制数177转换为八进制和二进制:
- 177 ÷ 8 = 22 余 1
- 22 ÷ 8 = 2 余 6
- 2 ÷ 8 = 0 余 2
逆序读取所记录的余数,得到的八进制数为261,而十进制数177的二进制等价数为10110001。
十六进制到十进制和十进制到十六进制的转换
十六进制到十进制
- 将十六进制数中的每一位数字乘以16的幂次方,并将它们相加。
- 计算结果即为十进制等价数。
2AF16 = 2 x (162) + 10 x (161) + 15 x (160) = 68710
十进制到十六进制转换
- 将十进制数重复除以16,直到商为0,记录每次的余数。
- 逆序读取所记录的余数,每个余数对应一个十六进制数字。
- 将这些十六进制数字连接在一起,即可得到对应的十六进制数。
转换 37810 to 十六进制数 和 二进制数:
|
Division |
Result |
Hexadecimal |
|
378/16 |
= 23+ remainder of 10 |
A (Least Significant Bit)23 |
|
23/16 |
= 1 + remainder of 7 |
7 |
|
1/16 |
= 0 + remainder of 1 |
1 (Most Significant Bit) |
|
Result |
37810 |
= 17A16 |
|
Binary |
= 0001 0111 10102 |
二进制到十六进制和十六进制到二进制的转换
二进制到十六进制转换:
- 将二进制数按照从右到左的顺序分组,每四位一组。如果最左边的组不足四位,则在左边补0。
- 将每个四位二进制组转换为对应的十六进制数。
- 将转换后的十六进制数按照从左到右的顺序排列,得到最终的十六进制数。
十六进制到二进制转换:
- 将十六进制数中的每一位转换为对应的四位二进制数。
- 将这些四位二进制数按照从左到右的顺序排列,得到最终的二进制数。
例如,让我们从二进制数10111011转换为十六进制数:
- 将二进制数按照四位一组分组:1011 1011
- 每个组转换为对应的十六进制数:B B
- 将转换后的十六进制数排列起来:BB
现在,让我们从十六进制数1F6转换为二进制数:
- 将十六进制数中的每一位转换为对应的四位二进制数:0001 1111 0110
- 将这些四位二进制数排列起来:000111110110
因此,二进制数10111011的十六进制等价数为BB,十六进制数1F6的二进制等价数为000111110110。
|
Hexadecimal Digit |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Binary Equivalent |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
Hexadecimal Digit |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
Binary Equivalent |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
每个十六进制数字确实由四位二进制数字表示。
例如:
假设我们有十六进制数字3A。
- 十六进制数字
3由二进制数字0011表示。 - 十六进制数字
A由二进制数字1010表示。
因此,十六进制数字3A的二进制表示为00111010。
1011 0010 11112 = (1011) (0010) (1111)2 = B 2 F16
八进制到十六进制转换
要将八进制转换为十六进制,首先可以将八进制数转换为二进制,然后再将二进制转换为十六进制。
例如,让我们将八进制数72转换为十六进制:
- 将第一个数字7从八进制转换为二进制:7在八进制中为111。
- 将第二个数字2从八进制转换为二进制:2在八进制中为010。
- 将这两个二进制数合并:111010。
- 将二进制数字分组,每四位一组,从右向左分组:0011 1010。
- 将每组四位二进制数转换为对应的十六进制数:3A。
- 因此,八进制数72的十六进制等价数为3A。
十六进制到八进制转换
要将十六进制转换为八进制,首先可以将十六进制数转换为二进制,然后再将二进制转换为八进制。
例如,让我们将十六进制数1B7转换为八进制:
- 将第一个数字1从十六进制转换为二进制:1在十六进制中为0001。
- 将第二个数字B从十六进制转换为二进制:B在十六进制中为1011。
- 将第三个数字7从十六进制转换为二进制:7在十六进制中为0111。
- 将这三个二进制数合并:0001 1011 0111。
- 将二进制数字分组,每三位一组,从右向左分组:001 101 101 111。
- 将每组三位二进制数转换为对应的八进制数:1557。
- 因此,十六进制数1B7的八进制等价数为1557。
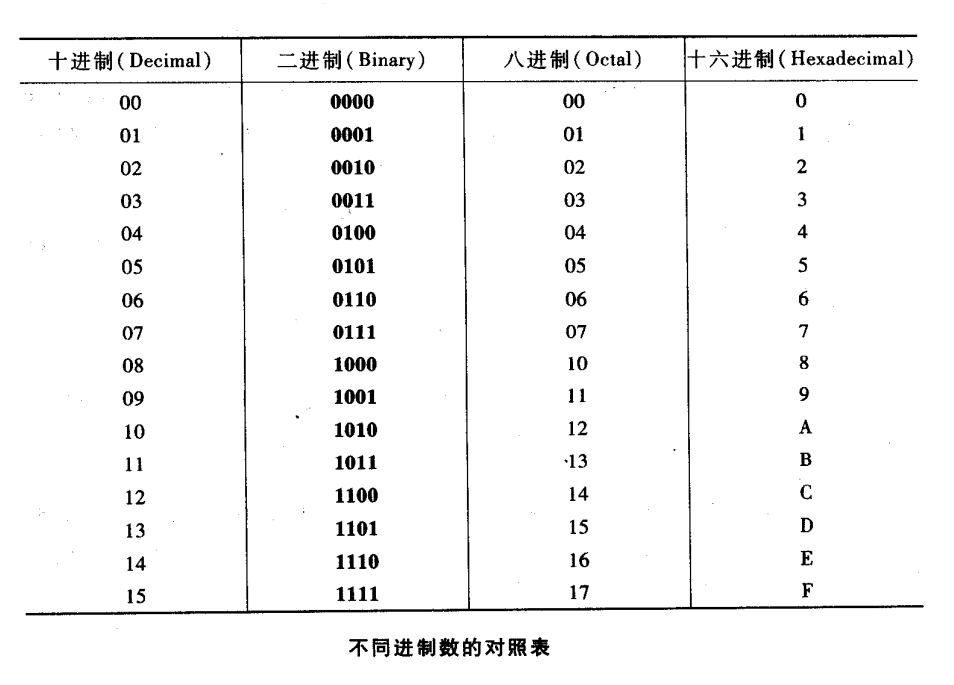
十进制十五以内不同进制等值数的对照表