错误检测和纠正码是用于在数字通信中检测和修正数据传输过程中发生的错误的编码方式。它们可以帮助识别和纠正由于噪声、干扰或其他传输问题引起的数据错误,提高数据传输的可靠性和稳定性。
错误检测码用于检测数据中的错误,而错误纠正码不仅可以检测错误,还可以通过相应的算法纠正错误。这些编码通常基于数学原理和算法,通过添加冗余信息到原始数据中来实现。在接收端,通过比对原始数据和冗余信息的校验结果来判断数据是否正确,并在可能的情况下进行纠正。
常见的错误检测和纠正码包括海明码、循环冗余校验(CRC)码、汉明码等。它们在各种通信和存储系统中广泛应用,如计算机网络、数字存储设备、卫星通信等领域。通过使用错误检测和纠正码,可以有效地保护数据的完整性和可靠性,确保数据的准确传输。
1. 错误检测码
当数据从一个点传输到另一个点时,比如在无线传输中,或者仅仅是存储在硬盘和内存中时,存在数据可能被损坏的情况。为了检测这些数据错误,我们使用特殊的编码,称为错误检测码。
奇偶校验码
在奇偶校验码中,每个数据字节或四位数据(根据用户的需求)都被检查是否具有偶数个1或偶数个0。基于这个信息,会在原始数据后附加一个额外的位。因此,如果我们考虑8位数据,添加奇偶校验位将使其变为9位长。
在接收端,再次计算奇偶校验,并与接收到的奇偶校验(第9位)进行匹配,如果匹配,则数据正常,否则数据被认为是损坏的。
奇偶校验有两种类型:
- 偶校验:检查是否有偶数个1;如果是,则奇偶校验位为零。当1的个数是奇数时,奇偶校验位设置为1。
- 奇校验:检查是否有奇数个1;如果是,则奇偶校验位为零。当1的个数是偶数时,奇偶校验位设置为1。
校验和(Check Sums)
在字节、字或双字上计算奇偶校验方法时,但是当需要在128字节或更多数据块上检查错误时(基本上是数据块),计算奇偶校验就不是正确的方法了。因此,我们有了校验和,它允许检查数据块中的错误。有许多校验和的变体。
最简单的校验和形式,即简单地将数据中的置位位相加,无法检测到许多类型的错误。特别是,这样的校验和不会受到以下情况的影响:
- 重新排列消息中的字节
- 插入或删除值为零的字节
- 多个错误之和等于零
校验和示例:给定4个字节的数据(可以使用任意数量的字节):25h、62h、3Fh、52h
将所有字节相加得到118h。 丢弃进位nibble得到18h。 获取18h的补码以得到E8h。这就是校验和字节。 要测试校验和字节,只需将其添加到原始字节组中。这应该给出200h。 再次丢弃进位nibble,得到00h。因为它是00h,这意味着校验和表示字节可能未更改。
2. 错误纠正码(Error-Correcting Codes,ECC)
错误纠正码(Error-Correcting Codes,ECC)不仅可以检测错误,还可以纠正它们。这通常在卫星通信中使用,因为回传延迟非常高,数据损坏的可能性也很大。
ECC(错误纠正码)也用于存储器、网络、硬盘、CD-ROM、DVD等领域。通常在网络芯片(ASIC)中,我们有2个错误检测位和1个错误纠正位。
这种技术在提高数据传输的可靠性和稳定性方面发挥着重要作用,特别是在对数据完整性要求较高的场景下,如存储器和通信系统。
汉明码(Hamming Code)
汉明码(Hamming Code),是在电信领域的一种线性调试码,以发明者理查德·卫斯里·汉明的名字命名。汉明码在传输的消息流中插入验证码,当计算机存储或移动数据时,可能会产生数据位错误,以侦测并更正单一比特错误。由于汉明编码简单,它们被广泛应用于内存(RAM)。
校验:
与其他的错误校验码类似,汉明码也利用了奇偶校验位的概念,通过在数据位后面增加一些比特,可以验证数据的有效性。利用一个以上的校验位,汉明码不仅可以验证数据是否有效,还能在数据出错的情况下指明错误位置。
纠错:
在接收端通过纠错译码自动纠正传输中的差错来实现码纠错功能,称为前向纠错FEC。在数据链路中存在大量噪音时,FEC可以增加数据吞吐量。通过在传输码列中加入冗余位(也称纠错位)可以实现前向纠错。但这种方法比简单重传协议的成本要高。汉明码利用奇偶块机制降低了前向纠错的成本。
校验方法:
汉明码(Hamming Code)是一种用于在嘈杂的信道中传输数据时最小化添加的位数,以便能够纠正每个可能的一位错误的编码方式。它可以检测(而不是纠正)两位错误,但不能区分一位和两位不一致。通常情况下,它不能检测到3位或更多位的错误。
其基本思想是,在n位字符串(我们称之为X)中的失败位位置可以用二进制表示为log2(n)位,因此我们只需尝试添加log2(n)位即可。
首先,我们将m = n + log2(n)设置为编码后的字符串长度,并且从1到m对每个位位置进行编号。然后我们将这些附加位放置在2的幂位置,即1、2、4、8…,而剩余的位(3、5、6、7…)保持原始顺序的位字符串。
现在,我们将每个添加的位设置为一组位的奇偶校验位。我们以以下方式对位进行分组:对于每个奇偶校验位,我们形成一个组,其中满足以下关系:
位位置(bit)AND 位位置(parity)= 位位置(parity)
(注意:AND是按位布尔AND运算符;奇偶校验位包含在组中;每个位可以属于一个或多个组。)
因此,位1组包含位1、3、5、7…,位2组包含位2、3、6、7、10…,位4组包含位4、5、6、7、12、13…以此类推。
因此,根据定义,X(上述失败位位置)是不正确奇偶校验位位置的总和(如果没有错误,则为0)。
要理解其原理,让我们将Xn表示X的二进制表示中的第n位。现在考虑每个奇偶校验位与X的一位相关联:
parity1 -> X1, parity2 -> X2, parity4 -> X3, parity8 -> X4
依此类推 – 对于程序员而言:它们是各自的AND掩码。通过构造,只有错误位会导致与X中的1相关联的奇偶校验位错误,因此如果相应的奇偶校验位错误,则X的每位为1,否则为0。
请注意,字符串越长,吞吐量n/m越高,而且不超过一个位失败的概率越低。因此,应将要发送的字符串分成块,其长度取决于传输通道的质量(通道越干净,块越大)。另外,除非保证每个块最多只有一个位失败,否则应添加校验和或其他形式的数据完整性检查。
3. 字母数字码(Alphanumeric Codes)
字母数字码(Alphanumeric Codes)是用于表示字母表中所有字母、数字和数学符号、标点符号的二进制码。这些码也被称为字符码。这些码使我们能够将输入输出设备(如键盘、打印机、视频显示器)与计算机进行接口连接。
ASCII码(ASCII Code)
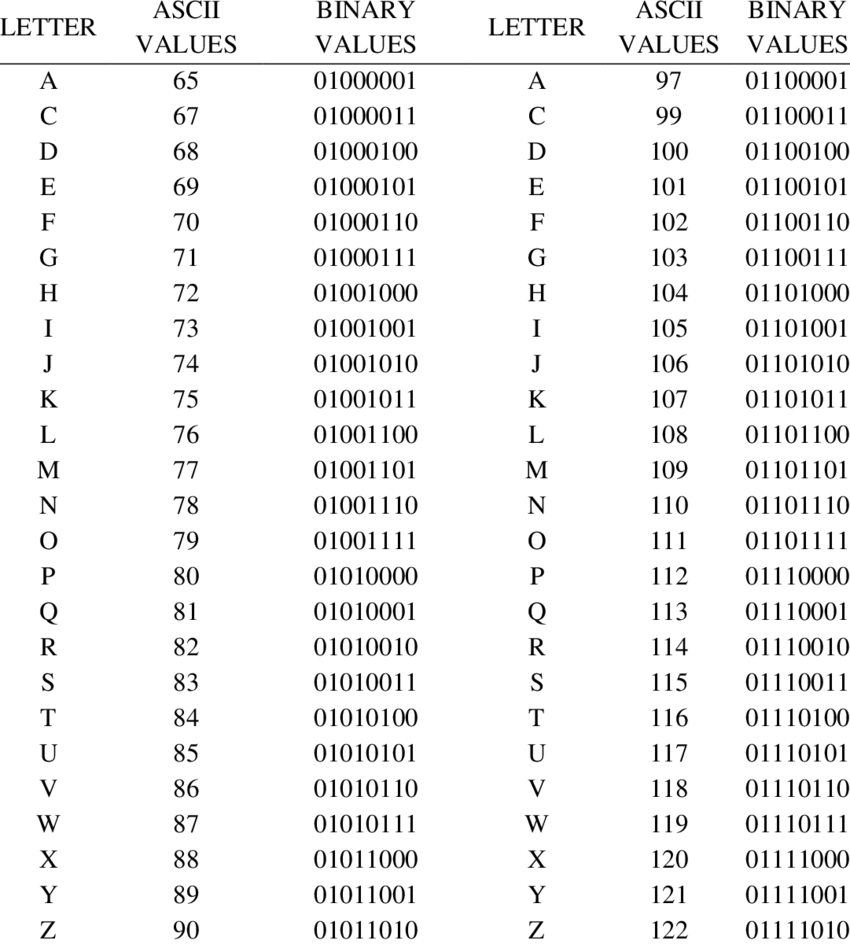
ASCII码(ASCII Code)代表美国信息交换标准代码(American Standard Code for Information Interchange)。它已成为微型计算机和计算机的世界标准字母数字码。它是一个7位码,表示128个不同的字符。这些字符包括26个大写字母(A到Z)、26个小写字母(a到z)、10个数字(0到9)、33个特殊字符和符号以及33个控制字符。
这7位码分为两部分,最左侧的3位部分称为区位码,右侧的4位部分称为数字码。
ASCII码的8位版本称为USACC-II 8或ASCII-8。8位版本最多可以表示256个字符。
详见: 美国信息交换标准代码
EBCDIC码(EBCDIC Code)
EBCDIC码(EBCDIC Code)代表扩展二进制编码的十进制交换码(Extended Binary Coded Decimal Interchange)。它主要用于大型计算机系统,如大型机。EBCDIC是一个8位码,因此可以容纳最多256个字符。一个EBCDIC码分为两部分:4个区位码(位于左侧)和4个数字码(位于右侧)。
