使用格雷戈里 – 莱布尼茨无穷级数。数学家们发现了若干个数学级数,如果实施无穷多次运算,就能精确计算出 Pi (π)小数点后面的多位数字。

其中部分无穷级数非常复杂,需要超级计算机才能运算处理。但是有一个最简单的无穷级数,即格雷戈里-莱布尼茨级数。
尽管计算较费时间,但每一次迭代的结果都会更接近 Pi 的精确值,迭代 500,000 次后可准确计算出 Pi 的 10 位小数。
公式如下:
π = (4/1) – (4/3) + (4/5) – (4/7) + (4/9) – (4/11) + (4/13) – (4/15) …
也可以用以下算式求出PI的值
PI/4 = 1-1/3+1/5-1/7+1/9-1/11…
无穷多次运算PI算法:
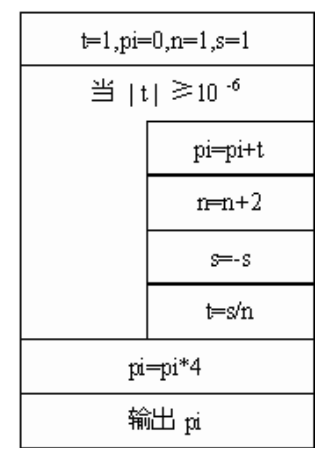
例1.PI的算法程序
#include<math.h>
main()
{
int s;
float n,t,pi;
t=1,pi=0;n=1.0;s=1;
while(fabs(t)>1e-5)
{
pi=pi+t;
n=n+2;
s=-s;
t=s/n;
}
pi=pi*4;
printf("pi=%10.5f\n",pi);
}
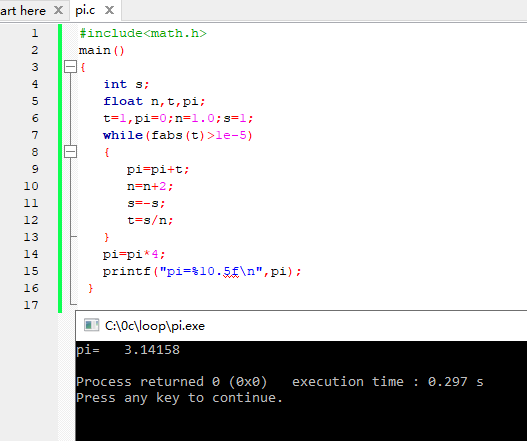
结果:
除教程外,本网站大部分文章来自互联网,如果有内容冒犯到你,请联系我们删除!
