什么是整数?
整数是可以有零、正和负值但没有小数值的整数。 例如,0、-5、10。 int 的大小通常为 4 个字节(32 位)。整数是将使用 4 字节(32 位)内存存储在计算机中的整数。
4字节整型的数值范围 -2147483648 到 2147483647 。
例如:
int a = 456;该值为 456。现在让我们将其转换为二进制。
256+0+64+32+0+0+4+0+0
1 0 1 1 0 0 1 0 0
现在你得到了 9 位数字。
由于 int 分配了 32 位,所以用 0 填充剩余的 23 位。
所以存储在内存中的值是
00000000 00000000 00000001 01100100
整型数据类型的分类
int a;
signed int a; // 等同于
int a;
unsigned int a; // 等同于
unsigned a;
signed char c; // 范围为 -128 到 127
unsigned char c; // 范围为 0 到 255
short int a; // 一般占用2个字节(整数范围为-32768~32767)。
long int b; //占用空间不少于int,至少为4个字节
long long int c; //占用空间多于long,至少为8个字节
unsigned short int a;
unsigned long int b;
unsigned long long int c;
short a; //C 语言允许省略int,所以变量声明语句也可以写成下面这样
unsigned short a; //C 语言允许省略int,所以变量声明语句也可以写成下面这样
long b; //C 语言允许省略int,所以变量声明语句也可以写成下面这样
unsigned long b; //C 语言允许省略int,所以变量声明语句也可以写成下面这样
long long c; //C 语言允许省略int,所以变量声明语句也可以写成下面这样
unsigned long long c; //C 语言允许省略int,所以变量声明语句也可以写成下面这样在 C 中,signed 和 unsigned 是符号类型修饰符,可以使用它们来更改数据类型的数据存储结构。
signed int a=2357;可以将该值转换成二进制数: 1 0 0 1 0 0 1 1 0 1 0 1 现在你得到了 12 位数字。 由于int分配了 32 位,所以用 0 填充剩余的 23 位。 所以存储在内存中的值是 00000000 00000000 00001001 00110101 例如:
unsigned int x;
int y;
这里,变量 x 只能保存零值和正值,因为我们使用了无符号修饰符。
考虑到 int 的大小是 4 个字节,变量 y 可以保存从 -2147483648 到 2147483647 的值,而变量 x 可以保存从 0 到 4294967295 的值。
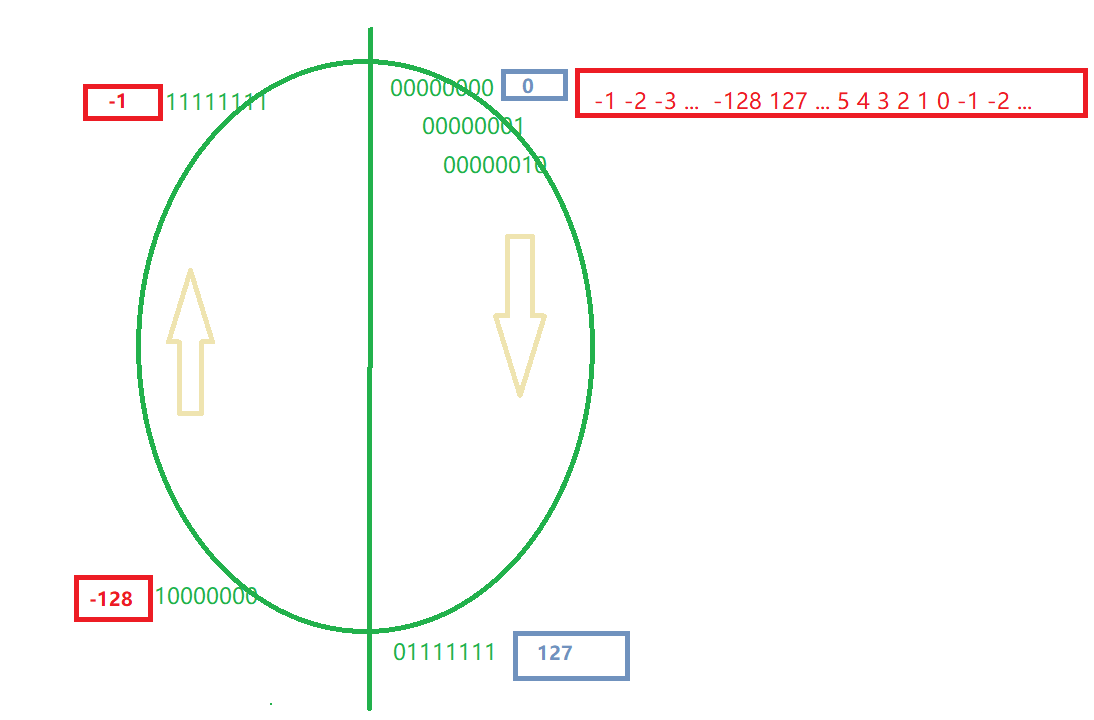
如何将正整数和负整数存储在计算机中?
计算机中的每个数据类型的存储都是以二进制形式存储,因为这是计算机唯一理解的语言。 其他语言如十进制是解释性的,机器必须将其翻译成二进制才能真正理解。
1.如何将正整数存储在计算机中?
例如,数字 4 是二进制的 100,如何将100放在4 个字节内存中:
00000000 00000000 00000000 00000100 0x0A 0x0B 0x0C 0x0D memory address C语言标准并不强制二进制以负数的形式存储,一般是以2的补码形式存储。 在N比特位的内存中,整数X的2的补码是2N - X。例如: 在8比特位的下,1的补码是28 - 1 或者说:1111 1111 在8比特位的下,8的补码是28 - 8 或者说:1111 1000 下例是十进制1和21的补码和反码,以及-1和-21在二进制的表达:
1 = 0000 0001
~1 = 1111 1110 (1's complement,反码)
~1 + 1 = 1111 1111 (2's complement,补码)
-1 = 1111 1111
21 = 0001 0101
~21 = 1110 1010 (1's complement,反码)
~21 + 1 = 1110 1011 (2's complement,补码)
-21 = 1110 1011补码比反码有几个优点。 例如,它没有“负零”的概念,负零的概念比较让人困惑;如果用补码,加法、乘法和减法对所有有符号整数的工作方式相同。
整形数据在内存中存放的就是补码
正数的原码、反码、补码相同。
正数和负数的二进制表达
我们先按最容易理解方式,如果二进制的工作原理和我们在处理负十进制值时习惯的一样:
第一个位置(位)表示符号(0 表示正,1 表示负),其他位表示数字 .
如果有 8 个比特位中,值 8 表示为 0 0001000,-8 表示为 1 0001000。
虽然我们很容易理解,但计算机很难使用,尤其是在做负数运算时。
数字在自然界中抽象出来的时候,一棵树,两只猪,是没有正数和负数的概念的
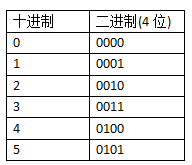
计算机保存最原始的数字,也是没有正和负的数字,叫没符号数字
如果我们在内存分配4位(bit)去存放无符号数字,是下面这样子的
后来在生活中为了表示“欠别人钱”这个概念,就从无符号数中,划分出了“正数”和“负数”
正如上帝一挥手,从混沌中划分了“白天”与“黑夜”
为了表示正与负,人们发明了”原码”,把生活应该有的正负概念,原原本本的表示出来
把左边第一位腾出位置,存放符号,正用0来表示,负用1来表示
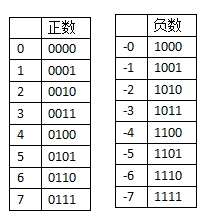
但使用“原码”储存的方式,方便了看的人类,却苦了计算机
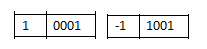
我们希望 (+1)和(-1)相加是0,但计算机只能算出0001+1001=1010 (-2)
这当然不是我们想要的结果;另外一个问题,这里有一个(+0)和(-0)。
为了解决“正负相加等于0”的问题,在“原码”的基础上,人们发明了“反码”
“反码”表示方式是用来处理负数的,符号位置不变,其余位置相反
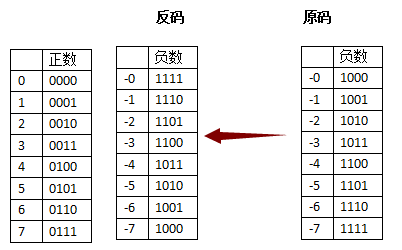
当“原码”变成“反码”时,完美的解决了“正负相加等于0”的问题
过去的(+1)和(-1)相加,变成了0001+1101=1111,刚好反码表示方式中,1111象征-0
人们总是进益求精,历史遗留下来的问题—— 有两个零存在,+0 和 -0
我们希望只有一个0,所以发明了”补码”,同样是针对”负数”做处理的
“补码”的意思是,从原来”反码”的基础上,补充一个新的代码,(+1)
我们的目标是(-0)
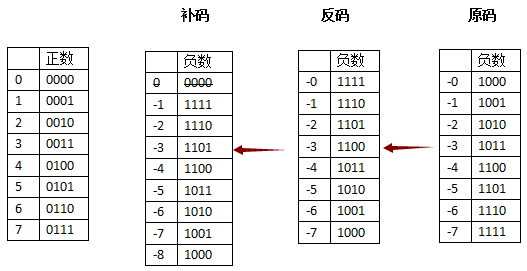
有得必有失,在补一位1的时候,要丢掉最高位
我们要处理”反码”中的”-0″,当1111再补上一个1之后,变成了10000,丢掉最高位就是0000,刚好和左边正数的0,完美融合掉了
这样就解决了+0和-0同时存在的问题
另外”正负数相加等于0″的问题,同样得到满足
举例,3和(-3)相加,0011 + 1101 =10000,丢掉最高位,就是0000(0)
同样有失必有得,我们失去了(-0) , 收获了(-8)。
以上就是”补码”的存在方式
反码
原码符号位不变,其他位按位取反。这使得在计算机上处理负数变得更容易,但复杂的是 +0 和 -0 有两种不同的表示形式。
如果有 8 个比特位中,十进制 8 表示为 00001000,-8 表示为 11110111。
补码是在反码的基础上加1。补码是当今最常用的负整数表示,因为它最容易用于计算机,但对于人类来说也是最难理解的。
例如,11111111 代表反码中的 -0,但补码代表 -1;在 8 位二进制补码中,值 8 表示为 00001000,-8 表示为 11111000。
举例说明整数65是如何存储的. 65 的二进制表达:1000001
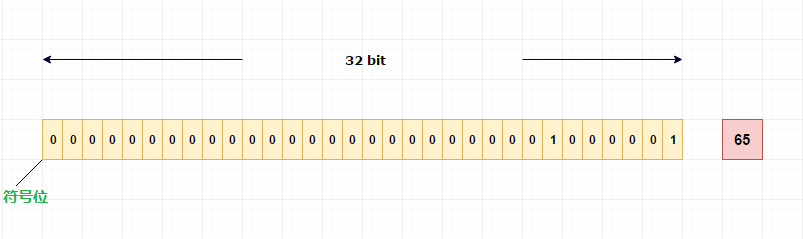
符号位0表示正整数,1表示负整数。
举例说明整数10和-10是如何存储的
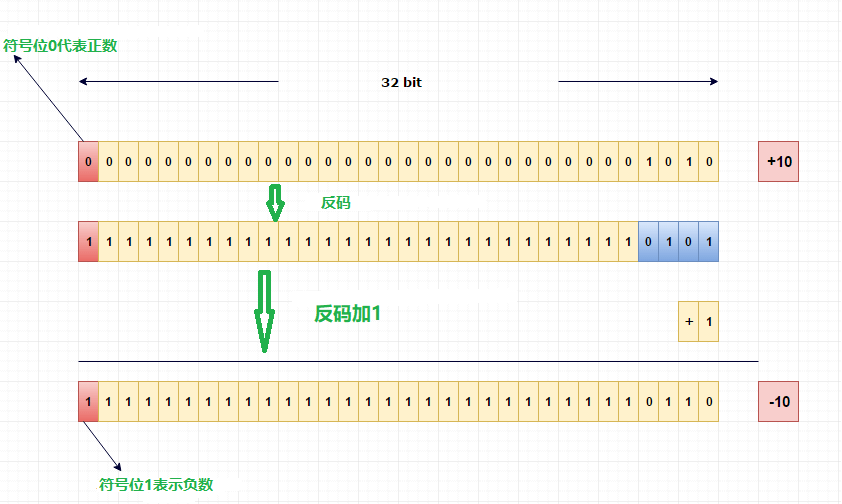
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值位统一处理。同时,加法和减法也可以统一处理(CPU只有加法器),此外,补码和原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
下图可以更好的理解比特位的溢出