数字数制是指用数字来表示数值的体系,其中最常见的包括:
- 十进制(Decimal):使用10个数字(0-9)表示数值的体系。每一位的权值是10的幂次方。
- 二进制(Binary):使用2个数字(0和1)表示数值的体系。每一位的权值是2的幂次方。
- 八进制(Octal):使用8个数字(0-7)表示数值的体系。每一位的权值是8的幂次方。
- 十六进制(Hexadecimal):使用16个数字(0-9以及A-F)表示数值的体系。每一位的权值是16的幂次方。
在数字系统中,每个数字位都代表一定的数值,而整个数字由这些数字位组成,通过各位的权值相加得到最终的数值。这些数字系统在计算机编程、数字电路设计等领域中有着广泛的应用。
十进制系统
十进制系统由10个数字或符号组成。这10个符号分别是0、1、2、3、4、5、6、7、8、9。利用这些符号作为数字,我们可以表示任何数量。十进制系统也称为以十为基础的进制系统,因为它有10个数字。
十进制是一种数制,也称为“基数10”,它使用10个数字符号(0、1、2、3、4、5、6、7、8、9)来表示数值。在十进制系统中,每个数字的权值是10的幂次方,从右向左依次增加,以10的0次方(即1)开始。例如,十进制数123表示为:
1 * 10^2 + 2 * 10^1 + 3 * 10^0
其中,1、2和3分别代表百位、十位和个位上的数字。十进制是我们日常生活和数学运算中最常用的数制。即使十进制系统只有10个符号,通过位置权重系统,可以表示任意大小的数字。
以下是十进制数的几个例子,包括整数、小数和负数:
- 整数:
- 123:百位1、十位2、个位3
- 1000:千位1、百位0、十位0、个位0
- 小数:
- 3.14:整数部分3,小数部分0.14(百分之一4,千分之一1)
- 0.5:半,相当于十进制的五分之一
- 负数:
- -10:负十,表示比零小10个单位
- -0.25:负零点二五,表示比零小0.25个单位
在十进制系统中,每一位的位置代表了不同的数量级,正数表示比零大的数,负数表示比零小的数。
十进制一般用小标10来代表:
- 3.1410
- 5210
- 102410
- 6400010
二进制系统
在二进制系统中,只有两个符号或可能的数字值,即0和1。这种基数为2的系统可以用来表示任何可以在十进制或其他进制系统中表示的数量。
|
23 |
22 |
21 |
20 |
2-1 |
2-2 |
2-3 |
|
|
=8 |
=4 |
=2 |
=1 |
. |
=0.5 |
=0.25 |
=0.125 |
|
最高有效位 |
二进制小数点 |
最低有效位 |
二进制计数序列显示在表格中,最后一列是十进制:
|
23 |
22 |
21 |
20 |
Decimal |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
2 |
|
0 |
0 |
1 |
1 |
3 |
|
0 |
1 |
0 |
0 |
4 |
|
0 |
1 |
0 |
1 |
5 |
|
0 |
1 |
1 |
0 |
6 |
|
0 |
1 |
1 |
1 |
7 |
|
1 |
0 |
0 |
0 |
8 |
|
1 |
0 |
0 |
1 |
9 |
|
1 |
0 |
1 |
0 |
10 |
|
1 |
0 |
1 |
1 |
11 |
|
1 |
1 |
0 |
0 |
12 |
|
1 |
1 |
0 |
1 |
13 |
|
1 |
1 |
1 |
0 |
14 |
|
1 |
1 |
1 |
1 |
15 |
二进制代表的信息
在数字系统中,通常以二进制形式呈现正在处理的信息。二进制量可以由任何只有两种操作状态或可能状态的设备表示。例如,开关只能打开或关闭。我们任意地(按照我们定义的方式)让打开的开关表示二进制0,闭合的开关表示二进制1。因此,我们可以通过使用一系列开关来表示任何二进制数。
典型的电压的二进制分配:
二进制1:在2V到5V之间的任何电压
二进制0:在0V到0.8V之间的任何电压
未使用:在5伏特CMOS和TTL逻辑中,0.8V到2V之间的电压不使用,这可能导致数字电路中的错误。如今的数字电路工作在1.8伏特,所以这个说法可能不适用于所有逻辑电路。
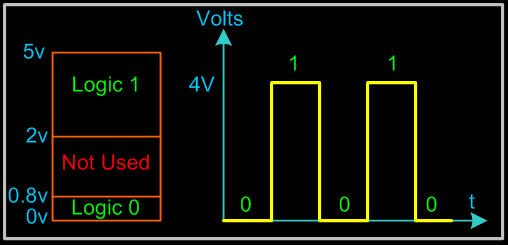
我们可以看到数字系统和模拟系统之间的另一个重要区别。在数字系统中,精确的电压值并不重要;例如,3.6V的电压与4.3V的电压意义相同。而在模拟系统中,精确的电压值很重要。
二进制数制是数字系统中最重要的一种,但还有其他几种数制也很重要。十进制数制很重要,是人类经常使用的数制系统但计算机不理解。这意味着在输入数字系统之前,需要将十进制值转换为二进制值。除了二进制和十进制之外,另外两种数制在数字系统中也有广泛的应用。八进制(基数为8)和十六进制(基数为16)数制也广泛应用。 这两种数制的应用目的就一个,更好的表达二进制系统。
八进制系统
八进制系统是一种以八为基数的数制,意味着它有八个可能的数字:0、1、2、3、4、5、6、7。八进制系统是一种数制,它以八为基数,即每一位的权值都是8的幂次方。在八进制系统中,使用八个数字(0、1、2、3、4、5、6、7)来表示数值。与十进制系统类似,八进制系统也使用位置权重的概念,每个数字位表示一定的权值,从右向左依次增加。八进制系统在计算机科学和数学等领域中有着广泛的应用。
|
83 |
82 |
81 |
80 |
8-1 |
8-2 |
8-3 |
|
|
=512 |
=64 |
=8 |
=1 |
. |
=1/8 |
=1/64 |
=1/512 |
|
最高有效位 |
八进制小数点 |
最低有效位 |
八进制数转换为十进制
将八进制数转换为十进制数的方法是将八进制数的每一位与相应的权值相乘,然后将它们相加。权值从右向左依次为8的幂次方,分别是0、1、2、3、…。以下是一个八进制到十进制的转换示例:
例如,我们有一个八进制数 257:
- 第一位(最右边)是 7,其权值为 8^0 = 1
- 第二位是 5,其权值为 8^1 = 8
- 第三位是 2,其权值为 8^2 = 64
然后,将每一位与相应的权值相乘并相加:
(2 * 64) + (5 * 8) + (7 * 1) = 128 + 40 + 7 = 175
因此,八进制数 257 转换为十进制数为 175。
更多的举例:
- 2378 = 2 x (82) + 3 x (81) + 7 x (80) = 15910
- 24.68 = 2 x (81) + 4 x (80) + 6 x (8-1) = 20.7510
- 11.18 = 1 x (81) + 1 x (80) + 1 x (8-1) = 9.12510
- 12.38 = 1 x (81) + 2 x (80) + 3 x (8-1) = 10.37510
十六进制系统
十六进制是一种数制,它以十六为基数,即每一位的权值都是16的幂次方。在十六进制系统中,使用16个数字来表示数值,包括0到9以及A到F,其中A到F分别代表十进制的10到15。与其他进制类似,十六进制也使用位置权重的概念,每个数字位表示一定的权值,从右向左依次增加。十六进制在计算机科学、数字电路设计和通信等领域中广泛应用,尤其在表示内存地址、颜色值和编码等方面。
|
163 |
162 |
161 |
160 |
16-1 |
16-2 |
16-3 |
|
|
=4096 |
=256 |
=16 |
=1 |
. |
=1/16 |
=1/256 |
=1/4096 |
|
最高有效位 |
十六进制小数点 |
最低有效位 |
十六进制到十进制转换
将十六进制数转换为十进制数的方法是将每一位与相应的权值相乘,然后将它们相加。权值从右向左依次为16的幂次方,分别是0、1、2、3、…。以下是一个十六进制到十进制的转换示例:
例如,我们有一个十六进制数 2F:
- 第一位(最右边)是 F,其权值为 16^0 = 1
- 第二位是 2,其权值为 16^1 = 16
然后,将每一位与相应的权值相乘并相加:
(2 * 16) + (15 * 1) = 32 + 15 = 47
因此,十六进制数 2F 转换为十进制数为 47。
更多的举例:
- 24.616 = 2 x (161) + 4 x (160) + 6 x (16-1) = 36.37510
- 11.116 = 1 x (161) + 1 x (160) + 1 x (16-1) = 17.062510
- 12.316 = 1 x (161) + 2 x (160) + 3 x (16-1) = 18.187510
十进制十五以内不同进制等值数的对照表
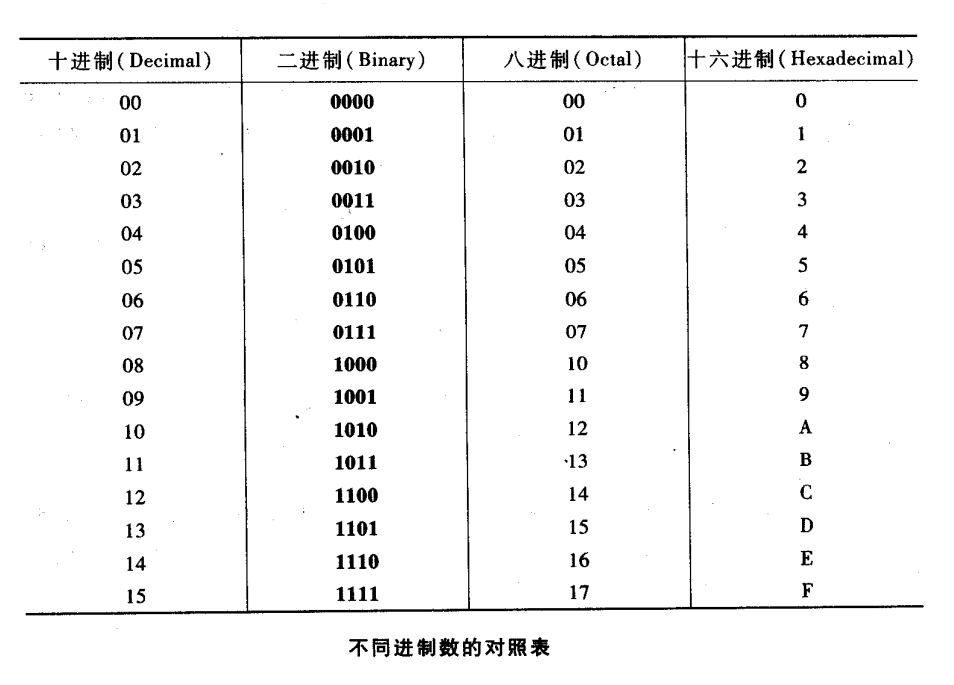
更多请看:

