1. 什么是递归？
递归是根据自身定义某些内容的过程。
一个物理世界的例子是放置两个相互面对的平行反射镜。 它们之间的任何对象都将递归地反映出来。
2. Python 递归函数
在 Python 中，我们知道函数可以调用其他函数。 函数甚至可能会自行调用。 这些类型的构造称为递归函数。
下图显示了称为recurse的递归函数的工作。
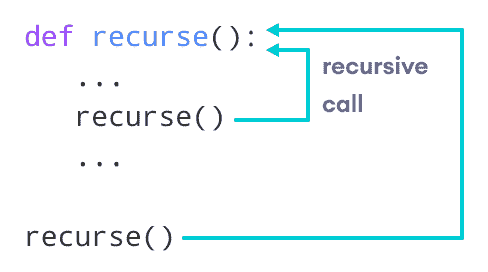
Python 中的递归函数需要有一个停止调用自身的条件。因此，您需要添加这样的 if 语句：
def fn():
# ...
if condition:
# stop calling itself
else:
fn()
# ...通常，您使用递归函数将难以解决的大问题划分为更容易解决的小问题。
例2.1 python中最简单的递归函数
假设您需要开发一个倒计时功能，从指定的数字倒计时到零。
例如，如果您调用从 3 开始倒计时的函数，它将显示以下输出：
3
2
1下面定义了 count_down() 函数：
def count_down(start):
""" Count down from a number """
print(start)如果你现在调用 count_down() 函数：
count_down(3)…它只会显示数字 3。
要显示数字 3、2 和 1，您需要：
- 首先，调用 count_down(3) 来显示数字 3。
- 其次，调用 count_down(2) 来显示数字 2。
- 最后，调用 count_down(1) 来显示数字 1。
为此，在 count_down() 函数内部，您需要定义一个逻辑来使用参数 2 和 1 调用函数 count_down()。
为此，您需要使 count_down() 函数递归。
下面定义了一个递归 count_down() 函数并通过传递数字 3 来调用它：
def count_down(start):
""" Count down from a number """
print(start)
count_down(start-1)
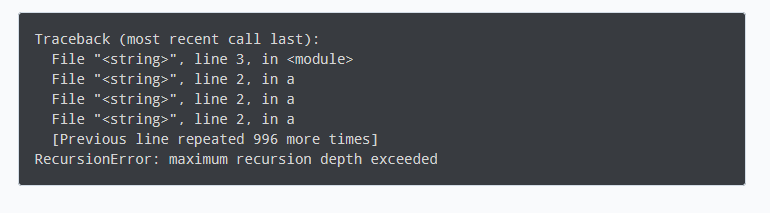
count_down(3)如果执行该程序，您将看到以下错误：
RecursionError: maximum recursion depth exceeded while calling a Python object原因是 count_down() 无限期地调用自己，直到系统停止它。
由于您需要停止倒计时，因此数字达到零。为此，您添加如下条件：
def count_down(start):
""" Count down from a number """
print(start)
# call the count_down if the next
# number is greater than 0
next = start - 1
if next > 0:
count_down(next)
count_down(3)结果
3
2
1在此示例中，count_down() 函数仅在下一个数字大于零时调用自身。换句话说，如果下一个数字为零，它就会停止调用自己。
例2.2 以下是查找整数的阶乘的递归函数的示例
数字的阶乘是从 1 到该数字的所有整数的乘积。 例如，阶乘 6（表示为6!）为1 * 2 * 3 * 4 * 5 * 6 = 720。
求阶乘的递归函数的范例
def factorial(x):
"""This is a recursive function
to find the factorial of an integer"""
if x == 1:
return 1
else:
return (x * factorial(x-1))
num = 3
print("The factorial of", num, "is", factorial(num))
results:
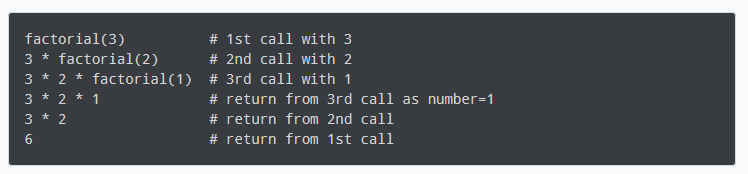
The factorial of 3 is 6在上面的示例中，factorial()是一个递归函数，它调用了自己。
当我们使用正整数调用此函数时，它将通过减少数量来递归调用自身。
每个函数将数字乘以其下面的数字的阶乘，直到等于 1。 可以在以下步骤中说明此递归调用。
让我们看一下显示发生了什么的逐步过程的图像：
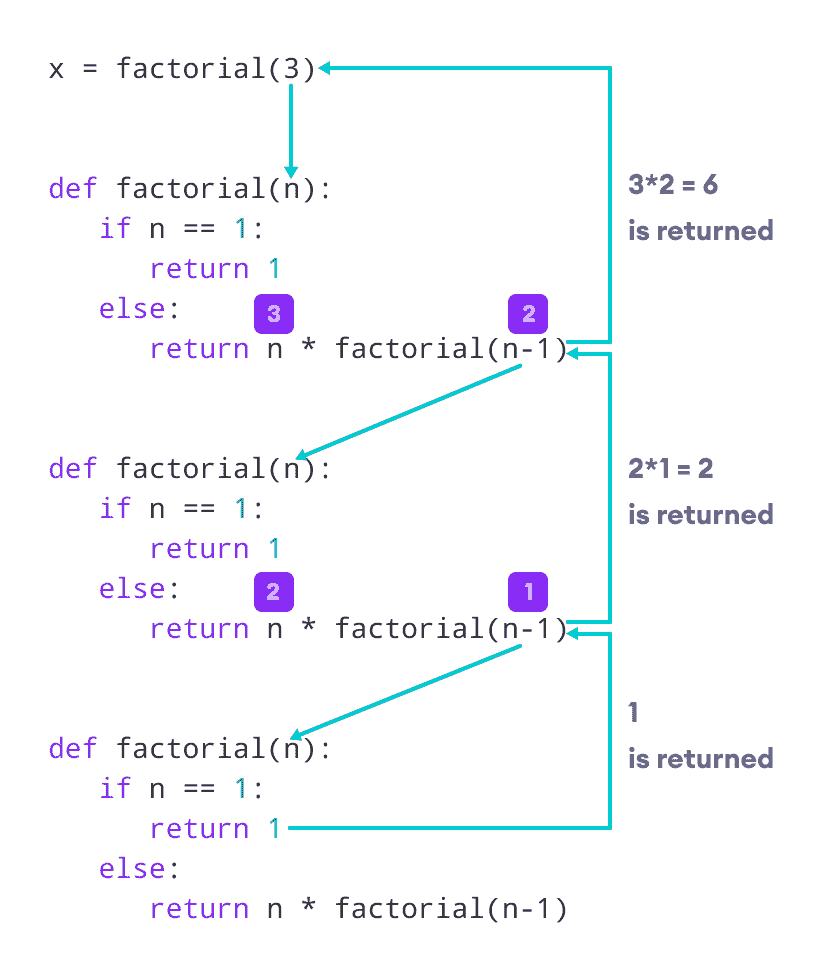
递归阶乘函数的原理
当数字减少到 1 时，我们的递归结束。这称为基本条件。
每个递归函数必须具有停止递归的基本条件，否则该函数将无限调用自身。
例2.3 使用递归函数计算一个序列的总和
假设您需要计算一个序列的总和，例如从 1 到 100。一个简单的方法是使用带有 range() 函数的 for 循环：
def sum(n):
total = 0
for index in range(n+1):
total += index
return total
result = sum(100)
print(result)Output:
5050要应用递归技术，您可以计算从 1 到 n 的序列之和，如下所示：
总和(n) = n + 总和(n-1)
总和（n-1）= n-1 + 总和（n-2）
…
总和（0）= 0
只要 sum() 函数的参数大于零，它就会一直调用自己。
下面定义了 sum() 函数的递归版本：
def sum(n):
if n > 0:
return n + sum(n-1)
return 0
result = sum(100)
print(result)如您所见，递归函数更短且更具可读性。
如果使用三元运算符，sum() 会更加简洁：
def sum(n):
return n + sum(n-1) if n > 0 else 0
result = sum(100)
print(result)Python 解释器限制了递归的深度，以帮助避免无限递归，从而导致栈溢出。
默认情况下，最大递归深度为 1000。 如果超出限制，则结果为RecursionError。 让我们看一个这样的条件。
def recursor():
recursor()
recursor()结果：
递归的优点
递归的缺点
