一、 陀螺仪结构原理与特性
高速转动的刚体称为陀螺,利用支撑架增加一个或两个自由度制作而成的陀螺仪具有特殊的性质:定轴性、进动性,利用这两个性质根据牛顿定律可以计算出某一方向的角速度。
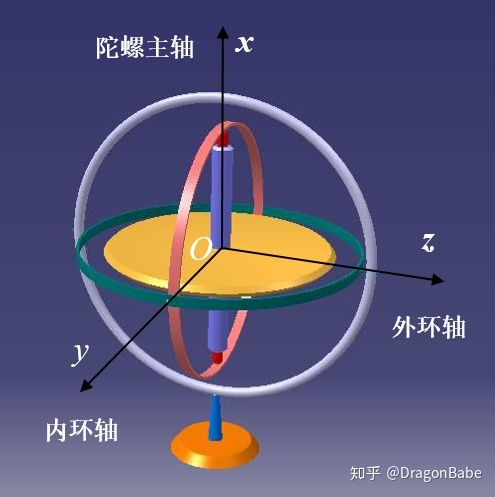
定轴性:高速运转的刚体在不受外力矩的作用下旋转轴方向相对惯性空间不变
进动性:陀螺仪转子高速转动时,陀螺仪内环轴方向受力后,陀螺主轴绕外环轴转动;外环轴方向受力后,陀螺主轴绕内环转动。这与转子静止时不同。
陀螺仪分为单自由度陀螺仪与双自由度陀螺仪,双自由度陀螺仪为陀螺转子增加了两个自由度,图1即为双自由度陀螺仪。单自由度陀螺仪为陀螺转子增加了一个自由度。具体如下图所示。
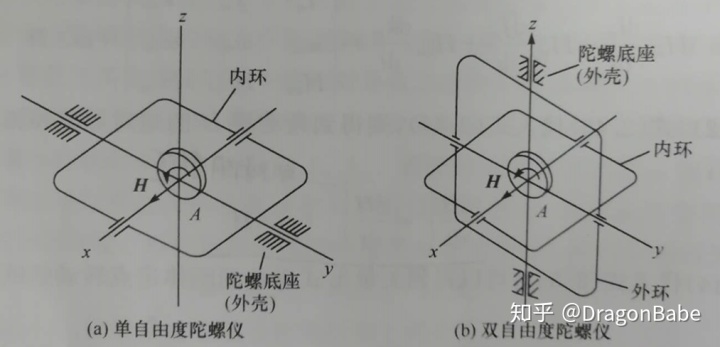
图2 单自由度与双自由度陀螺仪
两种陀螺仪均可敏感角速度,只不过陀螺仪进动性表现不同。下面以单自由度陀螺仪解释陀螺仪敏感角速度原理。
二、单自由度陀螺仪敏感角速度原理
单自由度陀螺仪给陀螺增加了一个自由度,共有两个自由度,结构可以建模成图3:
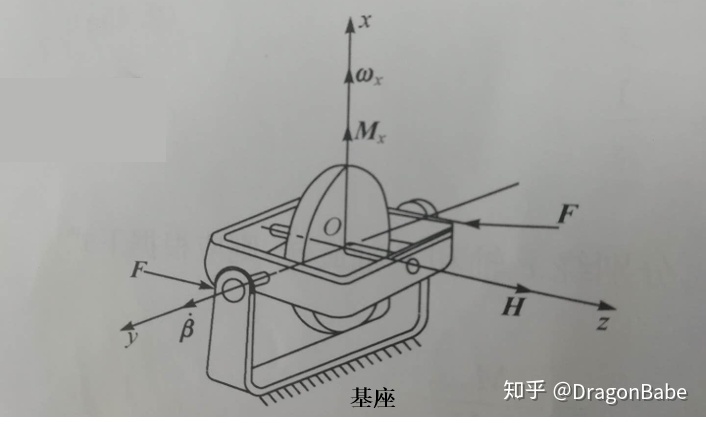
图3 单自由度陀螺仪模型
单自由度陀螺仪模型如图3所示, 分别为陀螺仪的三个周,
方向没有自由度。转子飞速转动的动量
沿
轴方向。当基座绕
轴转动或
轴转动时,由于内框架具有隔离运动作用,转子不会随着基座的转动而转动。当基座绕
轴转动时,内框架轴有一对力F作用在内框架轴的两端,形成力矩
,方向沿
轴方向。由于陀螺仪没有该方向的转动自由度,力矩
使陀螺仪绕内框架进动,沿
轴方向。总之,单自由度陀螺仪可敏感缺少自由度方向的角速度。
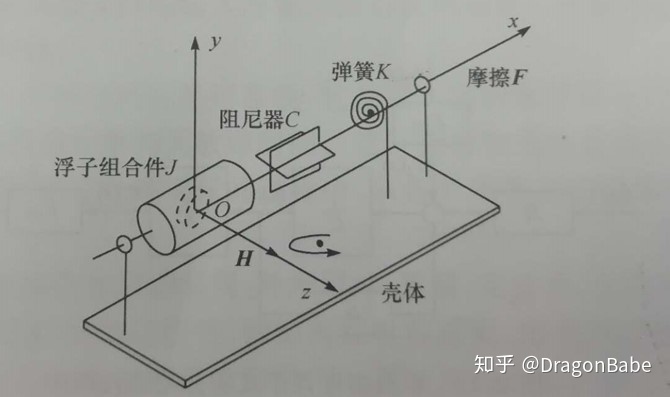
单自由度陀螺仪内部构造如图4所示。 轴为陀螺转子主轴(虚线为陀螺转子);
轴为缺少自由度的轴,也为输入轴;
轴为输出轴。由上述分析可知,
方向的角速度并不能使转子随着基座运动,即相对惯性空间不变;当且仅当
轴方向的角速度使的转子在
轴方向进动,即相对于惯性空间运动。
因此测量 轴的角速度即可测量载体在
轴的角速度。
总之,单自由度陀螺仪可以敏感某一轴相对惯性空间的角速度。
三、其他特性与定理(动量矩定理与陀螺表观运动)
陀螺仪利用陀螺的定轴性与进动性来敏感某一方向的角速度,具体计算时需要动量矩定理基础。
质点 的质量为
,速度为
,到空间点
距离为
,该质点对空间点
的动量矩
如下:
(1)
则绕 点转动的刚体对点
的质量矩
为:
(2)
注意是刚体所有质点的矢量和,对式(2)两边求导数得到:
(3)
式(3)右侧分为两项,第一项中 ,叉乘后为0,等式右边
,可得:
(4)
式(4)即为动量矩定理, 为合外力矩。表明动量的导数等于合外力矩。
实际研究过程中一般将刚体放于两个坐标系:惯性坐标系 与动坐标系
,动坐标系与刚体固连并且某一周沿着旋转主轴。利用动坐标系可以减小运算,根据两个坐标系的相对关系可以得到:
(5)
将式(5)中的坐标系改为地球坐标系 系,得到:
(6)
当合外力矩 时,得到:
(7)
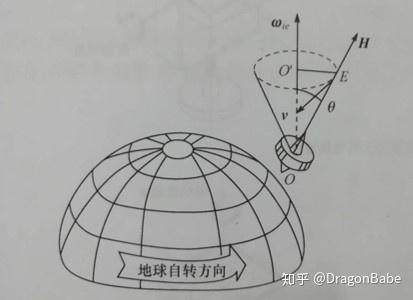
各物理量如图5所示。令 ,即为陀螺矢端线速度,即为:
(8)
同时,以地球自转轴为中心轴计算该线速度的角速度的标量表达式为:
(9)
方向沿 方向,因此:
(10)
上式表明,当陀螺转轴与地球自转轴存在角度 时,地球坐标系下直觉观看的表象运动为绕轴转动,转轴为与地球自转轴平行的轴。
